“7”: 七色彩虹, 七彩桥
English Version: Seven Colors of a Rainbow
> 彩虹有七种颜色。
说的准确些，彩虹的色谱是连续的。颜色带只是人眼的视觉效果。我们通常
说的七色（有牛顿总结提出）包含 赤，橙，黄，绿，蓝，靛，紫。
一周有七天，世界有七大奇迹。
> 我们从七的倒数（即 1/7，七分之一）开始。
1 / 7 = 142857 / 999999 = 0.142857142857141857 .. .. .. (一直重复下去)
注意数串142857 相当有趣，看一看下面的式子你就明白了:
1 × 142857 = 142857
2 × 142857 = 285714
3 × 142857 = 428571
4 × 142857 = 571428
5 × 142857 = 714285
6 × 142857 = 857142
7 × 142857 = 999999
注意到了吗？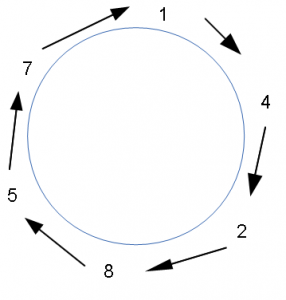
1 -> 4 -> 2 -> 8 -> 5 -> 7 好比一个神奇的圈，当乘数是1 – 6 时，我们仍然可以顺着圈读出结果，唯一不同的是从哪个数字开始。因而我们说这是一个叫人着迷的圆圈模式。
在右端的所有结果串中，数字 3，6，9 完全没有出现。如果注意到数字14：串的最左两位数字， 那么一个简单解释是：2 × 14 = 28 然后 3 × 14 = 42，所以数字3 没有机会出现。那要是 13 呢？你可以一试，不过可没有象 14 开头的串这么好的 Pattern。
> 假设你手里有标准的6面色子 （立方体，六面上分别有数字 1-6） 。同时掷两个这样的色子（或者掷两次），把出现的数字加起来得到和。和最可能是哪个数？是数字“7”。（如果先后两个数字是 1-6，2-5，3-4，4-3，5-2，6-1），求和的结果都是 7. 出现7的概率（可能性）是 1/6.
上述和的结果可能是 2 – 12 间的共11个数字。如果你把上面的实验做 110 次，那么出现7的次数会在 18次左右，而平均说来，11 个数字中的每个只有 10 次左右的机会。看出来了吧，出现“7”的机会确实多一些。
如果你把上面的实验真的做一次，也有可能观察到和上面分析相差较多的结果–因为是随机实验，结果当然也是完全随机的。
> 7 出现在Mersenne 数列中，
21 – 1, 22 – 1, 23 – 1, 24 – 1, 25 – 1, 26 – 1, 27 – 1, .. .. ..
Or
1, 3, 7, 15, 31, 63, 127
7 是第三个Mersenne 数. 3 (第三) and 7 都是素数。
已经证明，如果 n 不是素数，那么2n -1 也不是素数。相反的一面如何？如果 n 是素数，那么 2n – 1 一定是素数吗？我们现在知道这可不一定。不再继续讨论下去了，不过这是一个有趣的题目哦！
> 7 的四倍是 28。 请看下面的式子：
28 = 1 + 2 + 4 + 7 + 14
注意到右边的式子里面包含了28 的所有真约数，这表明 28 是完全数。
> 和七有关的说法：
七色彩虹，七彩世界
七情六欲，七上八下，乱七八糟
