π Ideas (1) a Fun Way of Finding the π Value
π Ideas for Circles and Trigonometry:
Stories, Facts and Implications
1st Story: A Fun Way of Finding the π Value
Here is some facts found in somebody’s math venture:
He marks a point A on a circle. He then split the radius of the same circle into 4 equal segments – call the length of one segment as b.
He measured along the circle using b (explain the measurement). After 7 steps he stopped and label that point as B. — As he noticed, the arc from A to B is slightly greater than a quarter of the circle.
Now he returns to split the radius of this circle into 5 equal parts – call the length of one segment as d. Then he measured along the circle using d. After 7 steps he stopped and label that point as D. — As he noticed, the arc from A to D is slightly less than a quarter of the circle.
Having a second look, he has noticed as well that the line connecting B and D “almost” passes through the centre of the circle (or line BD is “almost” a diameter).
Pause for a minute. Try to draw a diagram according to this description. If not sure, look into the figure below for a check.
pi-SmartRatio
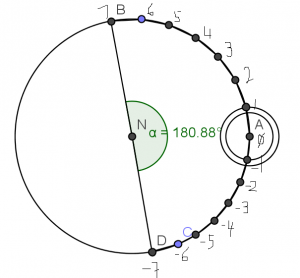
[As in this figure, N is the center of the circle, NA is the radius of the big circle, and the two small circles are of radius that is (1/4), resp. (1/5) of NA. From A, going through 7 steps to reach B; from A, going the other direction 7 steps to reach D. Pls. note the length of step in the two directions are not the same! ]
After some thought and calculation, he decided the approximate value of π. The value he’s found is 3.15 – which is pretty close to the true value. (For sure you know π is 3.14159, don’t you?)
Now is your chance to take part: how did he finds that value?
For a bonus question: he has decided that (7/4) radians is approximately 100 degrees. Do you agree? How did he come to that conclusion?
[Explain the concepts of radians if needed.]
